Algorithmen

Grundlagen

Logik

• $\iff$ bedeutet, dass die Behauptung links des Pfeils nur gilt, wenn (if and only if) die Behauptung rechts des Pfeils gilt

Summenregeln 🐝

• $\Sigma_{i=m}^na_i=a_m+a_{m+1}+...+a_n$
• $\Sigma_{i=1}^n i=\frac{n(n+1)}{2}$
• $\Sigma_{i=1}^n i^2=\frac{n(n+1)(2n+1)}{6}$
• $\Sigma_{i=1}^n c*a_i=c*\Sigma_{i=1}^n a_i$
• $\Sigma_{i=m}^n c = (n-m+1)*c$
• $\Sigma_{i=1}^n (a_i+b_i)=\Sigma_{i=1}^na_i + \Sigma_{i=1}^nb_i$
• $m^{log_mn}=n$

Logarithmus Regeln

• $log_bn=\frac{log_an}{log_ab}$
• $O(log_bn)*O(log_ab)=O(log_an)$
• $O(log_bn)*const=O(log_an)$
• $log_a(u*v)=log_au+log_av$
• $log_a\frac{u}{v}=log_au-log_av$
• $log_a(u^v)=v*log_au$
• $log_ab=n \Longleftrightarrow a^n=b$

Geometrische Reihe

• Für $|x| < 1$ gilt: $\sum\limits_{i=0}^{\infin}x^i=\frac{1}{1-x}$
• Ableiten und mit $x$ multiplizieren: $\sum\limits_{i=0}^{\infin}i*x^i=\frac{x}{(1-x)^2}$
• Für $\sum\limits_{k=0}^nar^k=ar^0+ar^1+ar^2...$ gilt $\sum\limits_{k=0}^nar^k=\frac{a-ar^{n+1}}{1-r}$

Rechenoperationen + Zifferstellen

• $Zahl+Zahl$: $n+1$ Ziffern, $n$ Grundoperationen
• $Zahl*Ziffer$: $n+1$ Ziffern, $2n+1$ Grundoperationen
• $Zahl*Zahl:$$n+1$ Ziffern $3n^2+n-1$ Grundoperationen
• $(a+b)^2$ => $2m+2$
• $a^2$ => $2m$
• $a+b$ => $m+1$
• Zahl plus Zahl

Schleifeninvariante

• Verträge bestehen aus

  • Vorbedingungen: Zusicherungen, die beim Aufruf des Algorithmus einzuhalten sind
  • Nachbedingungen: Zusicherungen, die am Ende des Algorithmus gelten
  • Invarianten: Schleifeninvarianten müssen vor/nach jeder Ausführung eines Schleifenkörpers gelten

• The loop invariant is a single condition or set of conditions that the algorithm maintains at the beginning, the end, and during each iteration of its execution

• The loop invariant for selection sort is that the elements of the newly sorted array up to the current index, A[0..i] will contain the i smallest elements of our original input, A[0..n-1]. They will also be in sorted order.

• The loop invariant for insertion sort states that all elements up to the current index, A[0..i], make up a sorted permutation of the elements originally found in A[0..i] before we began sorting.

Laufzeitanalyse von Algorithmen ⏳

Laufzeit von Code

Elementare Zuweisungen

• Variablendeklaration: String str;
• Initialisierung und Zuweisung: int i = j + 3;
• Vergleiche: if (j == 7)

Sequenzen von Anweisungen

• Laufzeiten für Sequenzen von Anweisungen werden addiert
• Verzweigungen werden addiert $O(f) + O(g)$, z.B. bedingte Blöcke (if) oder Fallunterscheidungen (switch)
• Schleifen werden multipliziert
• $c > 0$

Master-Theorem (Divide-And-Conquer) 👑

• $T(n) \leq \begin{cases} c &,n \leq 1 \\ a * T (\frac{n}{b})+f(n) & ,n > 1 \end{cases}$
• mit $c > 0, a >0, b>1, f(n) \in O(n^d), d\geq 0$ gilt
• $T(n) \in \begin{cases} O(n^d) &,d > log_ba \\ O(n^dlogn) &,d = lob_ba \\ O(n^{log_ba}) &,d < log_ba \end{cases}$

Landau Notation 🅾️

$f \in o(g)$

• $f$ wächst langsamer als $g$
• $lim_{x \to a}|\frac{f(x)}{g(x)}|=0$
• $\forall c > 0,\exists x_0 > 0 \forall x > x_0: |f(x)| < c * |g(x)|$

$f \in O(g)$

• $f$ wächst nicht wesentlich schneller als $g$
• $limsup_{x \to a}|\frac{f(x)}{g(x)}|<\infin$
• $\exists c > 0,\exists x_0 > 0 \forall x > x_0: |f(x)| \leq c * |g(x)|$

$f \in \Omega(g)$

• Asymptotisch untere Schranke $g \in O(f)$
• $liminf_{x \to a}|\frac{f(x)}{g(x)}|>0$
• $\exists c > 0,\exists x_0 > 0 \forall x > x_0: c * g(x) \leq |f(x)|$

$f \in \Theta(g)$

• Asymptotisch scharfe Schranke, sowohl $f \in O(g)$, als auch $f \in \Omega(g)$
• $0 < liminf_{x \to a}|\frac{f(x)}{g(x)}| \leq limsup_{x \to a}|\frac{f(x)}{g(x)}| < \infin$
• $\exists c > 0,\exists C > 0,\exists x_0 > 0 \forall x > x_0: c * |g(x)| \leq |f(x)| \leq C * |g(x)|$

$f \in \omega(g)$

• Asymptotisch dominant $g \in o(f)$
• $lim_{x \to a}|\frac{f(x)}{g(x)}|= \infin$
• $\forall c > 0,\exists x_0 > 0 \forall x > x_0: c * |g(x)| < |f(x)|$

Landau Notation Folgerungen

• $\Theta(f) \subseteq O(f)$

• $\Theta(f) \subseteq \Omega(f)$

• $\Theta(f) = O(f)\cap \Omega(f)$

• $\omega(f) \subseteq \Omega(f)$

• $o(f) \subseteq O(f)$

• $\Theta(f) \subseteq O(f)$

• $\emptyset= \omega(f) \cap o(f)$

   

Bekannte Ordnungen

O(log n)

• Since it takes linear time just to read the input, these situations tend to arise in a model of computation where the input can be “queried” indirectly rather than read completely, and the goal is to minimize the amount of querying that must be done
• E.g. binary search algorithm

O(n)

• One basic way to get an algorithm with this running time is to process the input in a single pass, spending a constant amount of time on each item of input encountered

• E.g. computing the maximum, merging two sorted lists into one sorted list

  max = arr[0]
  for i in range(1,len(arr)):
    if arr[i] > max:
      max = arr[i]
  return max
  

O(n log n)

• It is the running time of any algorithm that splits its input into two equal-sized pieces, solves each piece recursively, and then combines the two solutions in linear time

O(n²)

• Quadratic time arises naturally from a pair of nested loops

O(n^k)

• We obtain a running time of O(n^k) for any constant k when we search over all subsets of size k

Sortieren

Bubble Sort🛁

• Idee: Vergleiche Paare von benachbarten Schlüsseln und tausche, wenn linker Schlüssel größer ist als rechter

• Maximum wandert nach hinten

  xxxxxxxxxx
  int n = a.length;
  for i in range(0, i < n):
    for j in range (0, j < n-i-1):
      if (a[j] > a[j+1]):
        swap(a,j,j+1)
  

• Variable i: wieviele Elemnte am Ende sind schon soritiert

• Variable j: Nachbarschaftsvergleiche auf dem unsortierten "Rest"

• 🚢 Anzahl der Vergleiche : $\Sigma_{i=1}^n(n-1)=\Sigma_{i=0}^{n-1}i=O(n^2)$

• 🍓 Anzahl der Vertauschungen:

  • Best Case: 0 Swaps
  • Worst Case: $\frac{1}{2} (n^2-n)$ Swaps
  • Average Case: $\frac{1}{4} (n^2-n)$ Swaps

Insertion Sort🃏

• 🔑 Schlüssel: ​Zahlen die sortiert werden sollen

• Vergleichbar mit dem Sortieren von Spielkarten auf der Hand

  xxxxxxxxxx
  for i in range(1, len(arr)): 
          key = arr[i] 
          j = i-1
          while j >=0 and key < arr[j] : 
                  arr[j+1] = arr[j] 
                  j -= 1
          arr[j+1] = key 
  

• $i$ ist die "aktuelle" Karte die eingeordnet werden muss

  Algorithmus	Kosten	Anzahl
  for i = 2 to A.length	$c_1$	$n$
  key = A[i]	$c_2$	$n - 1$
  j = i - 1	$c_3$	$n - 1$
  while j > 0 and A[j] > key	$c_4$	$\sum^{n}_{i=2}t_i$
  A[j + 1] = A[j]	$c_5$	$\sum^{n}_{i=2}(t_i-1)$
  j = j - 1	$c_6$	$\sum^{n}_{i=2}(t_i-1)$
  A[j + 1] = key	$c_7$	$n - 1$

• $t_i$ = Anzahl der Ausführungen des while loop

• Der Test für for und while loops wird einmal öfter ausgeführt, als der Inhalt der Schleife

• $\sum^n_{i=2}i=\frac{n(n+1)}{2}-1$

• $\sum^n_{i=2}(i-1)=\frac{n(n-1)}{2}$

• Anzahl der Vergleiche:

  • Best Case: $O(n)$ bei sortierter Folge

    Average und Worst Case: $O(n^2)$

• Anzahl Verschiebeoperationen:

  • Worst Case: $\frac{n(n-1)}{2} \in O(n^2)$
  • Average Case: $\frac{n(n-1)}{4} \in O(n^2)$

Selection Sort

• Idee: Suche jeweils nächstes kleinstes Element

  • Durchlaufe die Folge von links nach rechts mit einem Zeiger i
  • Links von i sind die i-kleinsten Elemente sortiert
  • Finde in der verbleibenden menge das kleinste Element und tausche es mit i. Dann erhöhe i um eins
  • Tausche, falls linker Schlüssel größer ist als rechter

  xxxxxxxxxx
  public void selectionSort(int[] a) {
    for(int i = 0; i < a.length-1; i++) {
      int min = i;
      for(int k = i+1; j < n; j++) {
        if(a[j] < a[min])
          min = j;
      }
      swap(a,i,min)
    }
  }
  

• Anzahl der Vertauschungen:

  • Best Case, Worst Case, Average Case: $n-1$ Swaps
  • Lineares Wachstum

Merge Sort

• Idee: Rekursives Zerlegen der Eingabefolge in zwei gleichlange Folgen. Sortieren der Teillisten. Zusammenfügen.
• Höhe des Merge Sort Binärbaums: $h=log_2n$
• Master Theorem: $T(n)=\begin{cases} 1 & n \leq 1 \\ 2*T(\frac{n}{2})+f(n) & n > 1 \end{cases}$
• $log_ba=log_22=1$
• $f(n) = O(n)$, da beim Merge Schritt die beiden Folgen jeweils einmal von links nach rechts durchgegangen werden und auch maximal $O(n)$ viele Vergleiche benötigt. $O(n)=O(n^1) \to d=1$
• Zweiter Fall des Master Theorems: $O(n^d*logn)=O(n*logn)$

Quick Sort ⏩

• Idee: Optimierung von Merge Sort durch in-situ Sortieren

  • Wähle ein Pivotelement
  • Zerlegen in zwei Teilfolgen
  • Rekursiven Sortieren
  • Aufwand liegt im Divide Schritt, Merge Schritt ist lediglich Konkatenation

  ​x
  def quickSort(arr,low,high):
    if low < high:
      pi = partition(arr,low,high)
      quickSort(arr,low,pi-1)
      quickSort(arr,pi+1,high)
  ​
  def partition(arr,low,high):
    i = (low-1)
    pivot = arr[high] #could be random
    
    for j in range(low,high):
      if arr[j] <= pivot:
        i += 1
        arr[i], arr[j] = arr[j], arr[i]
     arr[i+1], arr[high] = arr[high], arr[i+1]
    return(i+1)
  

• Worst Case: Entarteter Baum

  • $T(n)=\begin{cases} T(n-1)+n-1 & n >1 \\ 0 & n=1 \end{cases}$
  • Mit Master Theorem gilt $T(n)=O(n^2)$

• Average Case: Jede Länge ist gleich wahrscheinlich, im Durchschnitt ist als die Länge der größten Teilfolge $L=2*\frac{1}{n}*\sum\limits_{i=\frac{n}{2}}^{n-1}i=\frac{3}{4}n-\frac{3}{2}$

• Pivot kann zufällig gewählt werden oder deterministisch mit dem Median-of-Medians Algorithmus in $O(n)$

• Pivot: The value within the partitioning space that I want to find a position for

• j: Scanning function

• i: Remembers the last position that an element was placed in, that was less than the pivotx

Quick Select

BFPRT

Heap Sort

• Binärbäume allgemein:

  • Ein vollständiger Binärbaum mit hat $2^h-1$ Kanten
  • Ein vollständiger Binärbaum mit hat $2^{h-1}$ Blätter
  • Ein vollständiger Binärbaum ist ein voller Binärbaum (alle Knoten haben entweder 2 oder 0 Kinder) in dem alle Blätter die gleiche Tiefe haben

• Heap Struktur: Binärbaum, der zwei Eigenschaften erfüllen muss

  • Links-vollständig (letzte Ebene kann von rechts her unvollständig sein)
  • Alle Vorgänger müssen größere (Max-Heap) oder kleinere (Min-Heap) Schlüssel haben als Nachfolger

• "Beinahe-Max-Heap" (die Max-Heap-Eigenschaft ist bei der Wurzel verletzt)

• Heapaufbau

  • Benötigt $O(n)$ Schritte
  • Nur die wenigen Knoten weit oben im Baum brauchen $log_2n$ Schritte
  • Vollständiger Binärbaum mit Höhe $h$ hat $n=2^{h+1}-1$ Knoten
  • Blätter ($2^h$) erfüllen immer die Heap Eigenschaft
  • In der Ebene darüber gibt es $2^{h-1}$ Knoten, die maximal einen Schritt versickern. Und so weiter.
  • Über alle Ebenen: $T(n)=\sum\limits_{i=0}^{h}(i*2^{h-i})=2^h*\sum\limits_{i=0}^{h}\frac{i}{2^i}$
  • Geometrische Reihe mit $x=\frac{1}{2}$: $\sum\limits_{i=0}^{\infin}\frac{i}{2^i}=\sum\limits_{i=0}^{\infin}i*(\frac{1}{2})^i=\frac{\frac{1}{2}}{(1-\frac{1}{2})^2}=2$
  • $2^h*\sum\limits_{i=0}^{h}\frac{i}{2^i} \leq 2^h*\sum\limits_{i=0}^{\infin}\frac{i}{2^i} \leq 2^h*2$
  • Damit gilt mit $n=2^{h+1}-1$: $T(n) \leq 2^{h+1} = n+1 \in O(n)$ //beide Seiten +1

• Heapify: Für jeden der $n$ Knoten (weil jeder mal Wurzel wird) wir gemacht

  • Tauschen mit dem letzten Knoten $O(1)$
  • Heapeigenschaft reparieren, Vertauschungen entlang eines Pfades im Baum, also $O(logn)$
  • Insgesamt: $O(n*logn)$

Schranken des Sortierproblems

• Können Sortierprobleme besser als $O(n*logn)$ sein?
• Beim Sortieren muss eine Teilmenge aus der Menge aller Permutationen der Liste gefunden werden
• Der Ablauf eines nur auf Vergleichen basierenden Sortieralgorithmus kann durch einen Entscheidungsbaum dargestellt werden (Anzahl der Blätter ist $n!$)

• Ein Baum der Höhe $h$ hat minimal maximal $2^h$ Blätter
• $n! \leq b \leq 2^h \to log_2{(\frac{n}{e})^n} \leq log_2n! \leq h = n*log_2n-n*log_2e$
• Damit gilt $\exists c > 0, \exists n_0 \in \mathbb{N} \forall n > n_0: h \geq c*(n*logn)$

Counting Sort 🧮

• Schlüssel sind darstellbar als ganzzahlige Werte im Bereich $0,...,m-1$
• Countingsort zählt, wie oft jeder dieser Werte in der Eingabe vorkommt. Diese Anzahlen speichert er in einem zusätzlichen Array mit $m$ Feldern ab. Mit Hilfe dieses Arrays wird anschließend für jeden Schlüsselwert die Zielposition in der Ausgabe berechnet
• Laufzeit- und Speicherkomplexität: $O(n+m)$
• Ungünstig bei großen $m$

Radix Sort

• Sei $m=B^d$ mit $B \ = \ Basis$ und $d \ = \ Anzahl \ Ziffern$
• Soritere das Eingabe Array $d$ mal nach aufsteigender Signifikanz der Stellen (braucht stabilen Sortieralgorithmus)
• Laufzeit: $O(d*(n+B))$

Suchen 🔍

Lineare Suche

• Jede Position eines Schlüssels ist gleichwahrscheinlich $\frac{1}{n}$
• Durchschnittliche Anzahl an Vergleichen ist $\sum\limits_{i=1}^{n}\frac{1}{n}*i=\frac{1}{n}*\frac{n*(n+1)}{2}=\frac{n+1}{2}$

Binäre Suche

• Suche einer Zahl in einer sortieren Zahlenfolge

xxxxxxxxxx
l = 0
r = n - 1
while (l <= r) do
  m = round((r + l) / 2)
  if A[m] == x then return m
  if A[m] < x then l = m + 1
  else r = m - 1
return -1

• Bei jedem Schleifendurchlauf halbiert sich der durchsuchte Bereich: $T(n)=T(\frac{n}{2})+1$
• Mit Master Theorem also $O(n^0*logn)$

Datenstrukturen

Vergleich

FIFO vs LIFO

• FIFO: Queue - enqueue / dequeue
• LIFO: Stack - push / pop

Dynamisches Array

• Array hat feste Größe

• push() Opertation normalerweise $O(1)$, wenn Array noch Platz hat, wenn nicht muss ein neues Array mit doppelter Größe alloziert werden. In diesem Fall müssen alle Elemente in das neue Array kopiert werden $O(m)$

• Reallozieren des Arrays auf halbe Größe, wenn das Array nur noch zu $\frac{1}{4}$ befüllt ist. pop() Operation also normal $O(1)$, mit Reallozieren $O(m)$

• Amortisierte Zeitanalyse für push() und pop()

  • Jedes push() und pop() bringen 5€ in die Kasse
  • 1€ für die normalen Kosten
  • 4€ werden gespart
  • Bei Reallokation sind dann also mindestens $4*(\frac{m}{4})=m$ € im System
  • $\frac{m}{4}$ weil der minimale Fall, dass eine Reallokation durchgeführt wird bei einem Füllgrad von $\frac{1}{4}$ stattfindet (halbierung des Array)
  • Mit den $m$ € kann dann eine Reallokation bezahlt werden
  • Die amortisierte Laufzeit ist also $O(1)$

Power dictionary

Prioritätswartschlange

• Datenstruktur, die es erlaubt das kleinste Element schnell zu finden und aus der Menge zu entfernen

• Mögliche Implementierung durch perfektem binären Baum, der die Heapeigenschaft erfüllt

• Baum erfüllt (Min-)Heapeigenschaft falls für jeden Knoten ausser der Wurzel der Schlüsselwert größer ist als der Schlüsselwert des Vaterknotens

  • MAKEQUEUE - O(1)
  • UNION - O(n)
  • MIN - O(1)
  • EXTRACT-MIN - O(logn)
  • INSERT - O(logn)
  • DELETE - O(logn)
  • DECREASE-KEY - O(logn)

Heaps

Binärer Heap

• Binärbaum, fehlende Blätter rechts unten

• Höhe $\lfloor{log n}\rfloor$

• Änderungen nur entlag eines Pfades Wurzel-Blatt

• insert()und deleteMin brauchen $O(logn)$

• min() dauert $O(1)$

• buildHeap() braucht $O(1)$

  • Sei $k=\lfloor logn \rfloor$
  • Sei Tiefe $l \in 0... \lfloor logn \rfloor$
  • $2^i$ Aufrufe von siftDown()
  • Kosten je $O(k-l)$
  • Insgesamt: $O(\sum\limits_{0\leq l\leq k}2^l*(k-l))=O(2^k*\sum\limits_{0\leq l\leq k}\frac{k-l}{2^{k-l}})=O(2^k*\sum\limits_{j\geq 1}\frac{j}{2^{j}})=O(2^k)=O(2^{logn})=O(n)$
  • $\sum\limits_{j\geq 1}\frac{j}{2^{j}}=O(1)$

Binomial Heap

• Sammlung von Binomialbäumen, jeder Baum ist ein Heap

• Es darf von jedem Grad nur einen Baum geben (merge trees of equal degree)

• In einem Binärbaum von Grad $k$ hat die Wurzel $k$ Kinder

• Der Baum hat Höhe $k$

• push() mit Worst Case $O(logn)$, amortisiert in $O(1)$. push() muss meistens nur auf kurzen Bäumen stattfinden

• decreaseKey() mit Worst Case $O(logn)$, da der Schlüssel eventuell bis nach ganz oben bubbeln muss

• popMin() mit Worst Case $O(logn)$

  • Wurzelelement entnehmen
  • Kinder auf höchste Ebene heben
  • Bäume gleichen Grades mergen

Hollow Heap

Fibonacci Heap

• Laufzeit

  • MAKEQUEUE - O(1)
  • UNION - O(1)
  • MIN - O(1)
  • EXTRACT-MIN - O(logn)
  • INSERT - O(1)
  • DELETE - O(logn)
  • DECREASE-KEY - O(1 am.)

Bäume

• Baum in Array transformierbar
• $parent(j)=\lfloor \frac{j}{2} \rfloor$
• $left \ child(j)=2j$
• $right \ child(j)=2j+1$

Binäre Suchbäume 🌲

• Eine Binärer Suchbaum muss die Form $value(v_i) \leq value(v_k) \leq value(v_j)$, wenn $v_i$ im linken Teilbaum und $v_j$ im rechten Teilbaum liegt

• ⛔️ Min-Heap: $value(v_k) \leq value(v_i) ,value(v_k) \leq value(v_j)$

• ⛔️ Max-Heap: $value(v_i) \leq value(v_k) ,value(v_j) \leq value(v_k)$

• Insert(key, value)

  • Suche den Schlüssel key im Baum
  • Falls key schon im Baum existiert, ersetze das vorherige Objekt
  • Falls nicht, hält die Suche in einem Blatt oder inneren Knoten mit max. einem Nachfolger
  • Füge einen neuen Knoten mit (key, value) als linker / rechter Folgeknoten bei diesem Knoten ein

• Remove(key)

  • Suche den Knoten $v$ Schlüssel key im Baum
  • Falls key schon im Baum existiert, passiert nichts
  • Falls $v$ ein Blatt ist, lösche den Zeiger darauf
  • Falls $v$ ein innerer Knoten ist, finde den rechtesten Knoten ( $v'$) im linken Teilbaum von $v$. Tausche $v$ mit $v'$. Lösche dann den Blattknoten $v$

• Änderungen im baum mit $O(1)$

• Suche der entsprechenden Position:

  • Maximale Anzahl Vergleiche entspricht maximaler Pfadtiefe des Baumes
  • Wenn $h(t)$ die Höhe des Baumes, Komplexität der Suche $O(h(t))$
  • $h+1 \leq n \leq 2^{h+1}-1 \ \ \to \ \ O(logn) \leq h \leq O(n)$
  • Worst Case: $O(n)$, Best Case: $O(logn)$

AVL-Bäume (Fibonacci Bäume) 🌴

• Binärer Suchbaum mit der Strukturbedingung: die Höhen der beiden Teilbäume unterscheiden sich höchstens um eins
• Das heißt, dass ein AVL Baum nicht maximal ausgeglichen sein muss, dafür ist er allerdings balanciert
• Um diese Bedingung aufrechtzuerhalten muss nach insert oder remove eventuell rebalanciert werden

• Wie hoch kann ein ABL-Baum für eine gegebene Knotenanzahl $n$ maximal werden?

• $N(h)$ ist die minimale Anzahl Knoten eines AVL-Baums der Höhe $h$

• Für beliebigen minimal gefüllten AVL-Baum der Höhe $h \geq 2$ gilt:

  • Wurzel besitzt zwei Teilbäume
  • Ein Teilbaum hat Höhe $h-1$
  • Der andere Teilbaum hat die Höhe $h-2$

• $N(h)=\begin{cases} 1 & h=0 \\ 2 & h=1 \\ N(h-1)+N(h-2)+1 & h > 1 \end{cases}$

• Ähnelt der Fibonacci Reihe. Deswegen $N(h)=fib(h+3)-1$

• $N(h) \leq n \Leftrightarrow h \leq log_{\psi}(n+1)+const$

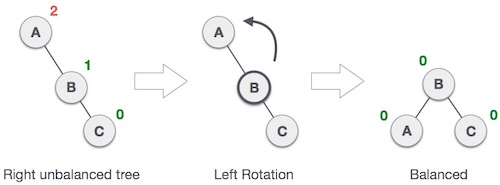
• Links-links Rotation bei Einfügung in Teilbaum "rechts rechts"

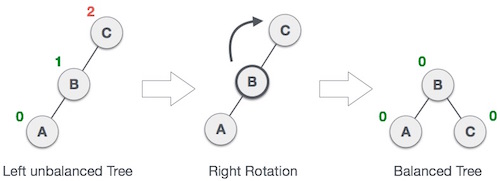
• Rechts-rechts Rotation bei Einfügung in Teilbaum "links links"

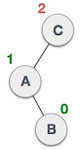
• Links-rechts Rotation bei Einfügung in Teilbaum "links-rechts"

  

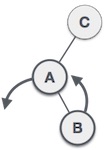
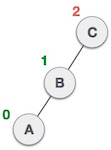
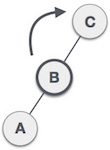
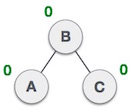
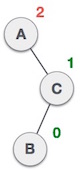
• Rechts-links Rotation bei Einfügung in Teilbaum "rechts-links"

  

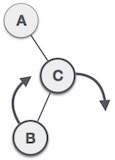
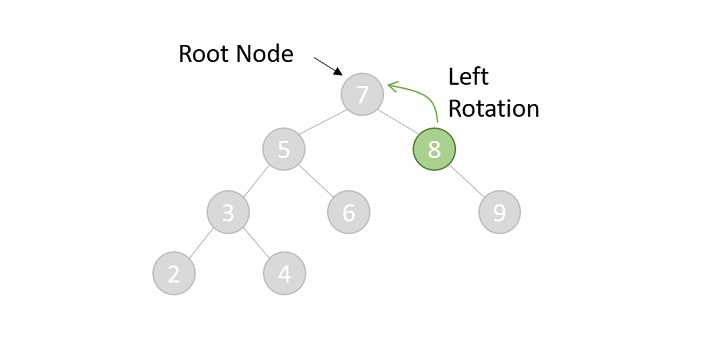
• Rotationen brauchen konstante Zeit $O(1)$, Einfügen mit Rebalancierung also $O(h) + O(1) = O(logn)$

• Beim Löschen kann es passieren, dass man den ganzen Pfad entlag Rebalancierungen vornehmen muss, maximal also $h$ Rotationen. Löschen mit Rebalancierung also im Worst Case $O(logn) + O(logn) = O(logn)$

• Beinahe AVL-Baum: Nur an der Wurzel um $1$ debalanciert

•  

Hash Tabelle 🌿

Grundlagen des Hashing

• Idee: Abbilden verschiedener Schlüssel auf dieselben Indexwerte. Kollisionen möglich
• $U:$ Universum aller Schlüssel
• $S \subseteq U:$ Menge der zu speichernden Schlüssel mit $n = |S|$
• $T:$ Hash-Tabelle mit $m = |T|$
• $h: U \to (0,...,m-1)$ ist die Hashfunktion, die den Indexwert berechnet
• $\alpha = \frac{n}{m}$ ist der Belegungsfaktor
• Die Hashfunktion muss surjektiv sein

Perfekte Hashfunktion 👌

• Eine Hashfunktion ist perfekt wenn $h(k_i)=h(k_j) \iff i=j$
• Eine Hashfunktion ist minimal wenn $m=n$

Kollisisionswahrscheinlichkeit

• Wahrscheinlichkeit, dass es zu einer Kollision kommt ist $P(NoCol|n,m)=\prod\limits_{i=0}^{n-1}(1-\frac{i}{m})$
• Kollisionswahrscheinlichkeit bleibt konstant wenn $m$ quadratisch mit $n$ wächst

Offenes Hashing mit geschlossener Adressierung ⛓

• Speicherung der Schlüssel als verkettete Liste
• Worst Case: Suche mit $O(n)$, das heißt eine ganz lange verkette Liste mit allen $n$ Elementen
• Average Case: Suche mit $\Theta(1+ \alpha)$ unter der Annahme von Gleichverteilung
• Worst Case: Einfügen mit $O(1)$, immer am Anfang der Liste
• Worst Case: Löschen mit $Laufzeit \ Suche + O(1)$ (Erklärung für Löschlaufzeit)

Geschlossenes Hashing mit offener Adressierung

Polynomielles Sondieren

• Für $j=0...m$ teste Hashadresse $h(x,j)=(h(x)+c_P*j^P)\ mod \ m$ bis eine freie Adresse gefunden wurde
• Lineares Sondieren: $P=1$, also $h(x,j)=(h(x)+c*j)$
• Quadratisches Sondieren: $P=2$, also $h(x,j)=(h(x)+c*j^2)$

Doppelhashing

• Nutzung zweier unabhängiger Hashfunktionen

  • $P(h(x)=h(y))=\frac{1}{m}$ und $P(h'(x)=h'(y))=\frac{1}{m}$
  • $P(h(x)=h(y) \ \and \ h'(x)=h'(y))=\frac{1}{m^2}$

• Sondierung mit $h(x,j)=(h(x)+h'(x)*j^2) \ mod \ m$

Suchen nach Löschen

• Offenes Hashing: Behälter suchen und Element aus Liste entfernen
• Geschlossenes Hashing: Behälter suchen und Zelle als gelöscht markieren. Notwendig, da evtl. bereits hinter dem gelöschten Element andere Elemente durch Sondieren eingefügt wurden

Universelles Hashing

• Sei H eine endliche Menge an Hashfunktionen von $U$ nach $\{0,1,...,t −1\}$. H ist universell falls für $a,b \in U$ mit $a \neq b$ die Anzahl der Hashfunktionen $h \in$ H mit $h(a) = h(b)$ höchstens $\frac{|H|}{|T|}$ ist.
• Wahrscheinlichkeit einer Kollision mit höchstens $\frac{|T|}{|H|}$

Graphen 📈

Allgemeines

• $V:$ Menge der Knoten mit Knotenanzahl $|V|$
• $E:$ Menge der Kanten mit Kantenanzahl $|E|$
• $|E| \leq |V|^2$
• Grad eines Knoten ist die Anztahl der ein- und ausgehenden Kanten
• $u \to v = [u,v \rangle$
• $u \leftrightarrow v = u - v = \{u,v\}$
• DAG: Quelle = Knoten mit Eingangsgrad Null, Senke = Knoten mit Ausgangsgrad Null

Darstellung

Adjazenzmatrix

• $A$ ist eine boolsche Matrix mit $A_{ij}=\begin{cases} true && falls \ (v_i,v_j) \in E \\ false && sonst \end{cases}$
• Entscheidung, ob $(i,j) \in E$ in $O(1)$
• Platbedarf und Inititalisierung stets $O(|V|^2)$
• Anstelle von boolschen Werten können auch Zusatzinformationen (z.B. Kosten) in Matrix gespeichert werden

Adjazenzliste

• Entscheidung, ob $(i,j) \in E$ im Average Case mit $O(\frac{|E|}{|V|})$
• Platzbedarf und Initialisierung von $O(|V| + |E|)$

Graph-Durchlauf

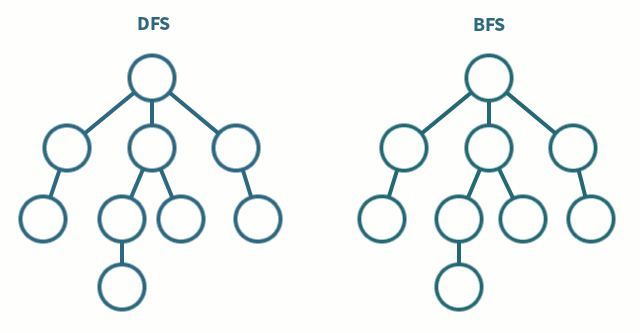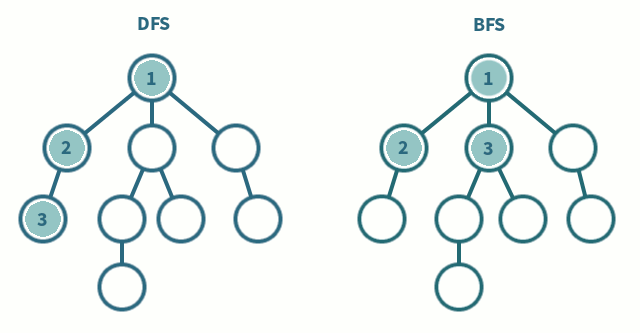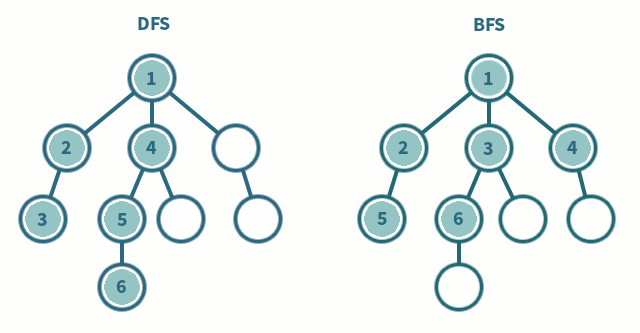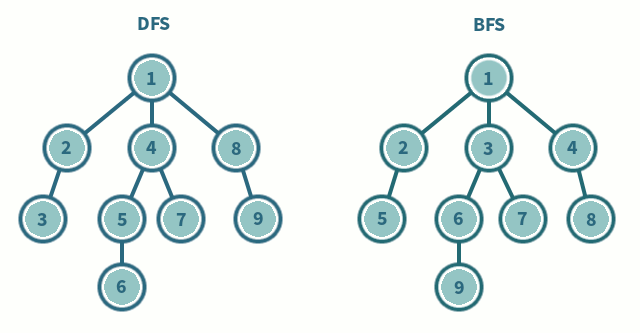
• Zeitkomplexität: $O(|V|+|E|)$
• Speicherkomplexität: $O(|N|)$